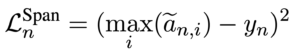This is a guest post from Joe Stacey about our quest to create interpretable Natural Language Inference (NLI) models. In this post he will share some of our ideas about interpretability, introduce the idea of atomic inference, and give an overview of the work in our 2022 and 2024 EMNLP papers [1,2]. At the end he’ll also share some of the other relevant papers that have inspired us along the way.
The goal of creating interpretable, high performing models
The focus of our research has been trying to create interpretable models that still perform competitively. After all, surely it’s better to have an interpretable model, where you can understand the reasons for each model prediction, rather than trying to interpret a black-box model (with no guarantees of faithfulness). Even though creating high performing, interpretable models seems like a sensible thing to want to do, there is little research in this area. A recent survey paper by Calderon and Reichart [10] found that less than 10% of NLP interpretability papers consider inherently interpretable self-explaining models, with the authors advocating for more research on causal based interpretability methods.
Maybe it’s just too difficult to create interpretable models that also perform competitively? Our findings suggest that this isn’t the case, and we hope to convince you that trying to create more interpretable models is an exciting and worthwhile area of research (which could be of real benefit to the NLP community).
Atomic Inference, and why we think it’s important
Our efforts to create interpretable models have centred around methods that we describe as Atomic Inference. I’ll start by explaining what this means, and why we felt that we needed to introduce this term.
We use the term atomic inference to describe methods that involve breaking down instances into sub-component parts, which we describe as atoms (sounds cool, right?), with models independently making hard predictions for each atom. The model’s atom-level predictions are then aggregated in an interpretable way to make instance-level predictions. This means that we can trace exactly which atoms are responsible for each model prediction. We refer to this as a faithfulness guarantee, as we can be certain which components of an instance were responsible for each prediction.
You might be wondering, what happens if we need to make a prediction based on two different atoms? How can we do that if the predictions for each atom need to be independent? One option is to create an additional, new atom that contains all of the relevant content from the other atoms that you need to combine.
We felt we needed to introduce the term atomic inference to distinguish interpretable atom-based methods from other work that doesn’t have the same interpretability benefits, for example when the atomic decomposition is introduced in order to improve model performance.
There are some key parts of the atomic inference definition that separate these methods from other atom-based methods:
- Atomic inference methods require models to make each atom-level prediction independently, or in other words, predictions for one atom do not also have access to the content of the other atoms. This is often not the case for other atom-based methods [3, 4, 5]. By making the atom-level predictions independently, we guarantee that the content of each atom is the reason for the corresponding atom-level predictions. Otherwise, we no longer have our faithfulness guarantee.
- Atomic inference also requires hard predictions for each atom. Instead, other methods can require soft probability scores (for example considering a mean score from each atom [6, 7, 8]). If the end goal is improving model performance, using soft probability scores makes a lot of sense. But if your goal is to improve interpretability, making hard predictions for each atom has considerable advantages, pinpointing the specific atoms that are responsible for each prediction.
So, in the end, atomic inference methods give us a faithfulness guarantee – we know, for certain, which atoms are responsible for each model prediction. Although, admittedly, the predictions for each atom remain a black-box. But in our opinion, this is fine! Atomic inference methods may not be perfect, but they are useful and practical interpretability methods.
This sounds intriguing! I get the idea, but how does this work in practice?
Great question! Let me walk through our EMNLP 2022 paper to give you a flavour of what atomic inference methods can look like in practice. The work focuses on NLI, but the same method could also be applied to other, similar tasks.
In this paper we proposed the idea that we could decompose NLI instances into atoms by segmenting the hypotheses into different spans, with each span being described as an atom. You can see the example below, where the hypothesis is segmented into spans. In this example, each span can be considered as an entailment span, except for the final span, which is neutral with respect to the premise (we don’t know if the man is carrying a surfboard or not).
We created the spans by segmenting the hypothesis based on the presence of nouns, but in our experience changing how we segment the text into spans didn’t make so much difference.
The tricky part is what to do when you have some kind of long range dependence across the sentence, e.g. if you have a negation word at the beginning of the sentence that will impact other spans towards the end of the input. Or perhaps you need to consider multiple spans together to correctly deduce the entailment relationship. To overcome these issues, we considered including consecutive spans as additional atoms (the number of consecutive spans we combine was a hyper-parameter). It’s not the perfect solution, but it was good enough for high performance on SNLI. We therefore had overlapping atoms, with single spans being considered as atoms alongside consecutive spans. While this might seem a bit unusual, the presence of overlapping (or duplicate) atoms isn’t a problem for atomic inference systems.
Next I’m going to talk about how inference works, and how we combine the model predictions for each individual atom to get a prediction for each instance. After that we’ll get to the problem of how to train a model to make accurate predictions for individual atoms (when we don’t have any atom-level labels to train with).
How inference works with our EMNLP 2022 paper
Our model makes predictions of either entailment, neutral or contradiction for each atom (our spans). We then aggregate these span predictions together using the following logic:
- If any span in the hypothesis contradicts the premise, then the entire hypothesis will contradict the premise
- Otherwise, if any span in the hypothesis is predicted as neutral, then the hypothesis is neutral with respect to the premise
We provide an example below where the model predicts the neutral class:
In this case, the model predicts the following spans as being neutral: “the sisters”, “are hugging goodbye” and “after just eating lunch”. As we have no contradiction spans being predicted, and there is at least one neutral span, the prediction must be neutral overall. Moreover, we know exactly why the model is making this prediction – because two women aren’t necessarily sisters, embracing doesn’t necessarily mean hugging goodbye, and we don’t know if the women have just had lunch.
Our co-author Haim Dubossarsky once described this as “giving a model explainability super-powers” – because with the atomic inference faithfulness guarantee, we know exactly why the model made each prediction (up to an atom-level).
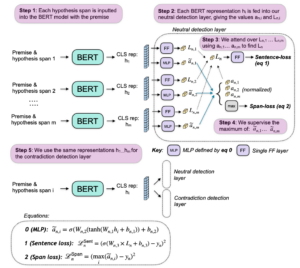
Model training in our EMNLP 2022 paper
Now that we’ve sorted out how things work during inference, we need to face the tricky problem of how to train models to make accurate predictions for each specific span. We only have labels at an instance-level, and we want to avoid having to manually annotate spans to obtain span-level training data. Instead, our idea is to use a semi-supervised method where the model decides for itself which spans are likely to be neutral or contradiction. Specifically, during training we encode the premise together with each hypothesis span in turn, with a simple MLP giving us a neutral score for every atom in the instance. We then supervise the maximum of these neutral scores, comparing this to a binary neutral label of 1 or 0 (if we are expecting there to be a neutral span present or not).
This involves considering the following loss:
Where i are the atoms for that instance, n refers to the neutral class, \(y_n\) is the binary neutral label. \(\widetilde{a}_{n,i}\) is the neutral score for each atom.
We then follow the same process for contradiction, finding a contradiction score for each atom, and then supervising the maximum score for each instance. As with the neutral class, we compare this maximum score to a binary label of 1 or 0 based on if we are expecting there to be a contradiction span.
What remains is how to decide what these binary neutral and contradiction labels should be during training. To do this, we introduce even more rules that govern the interaction between the instance labels and the span labels:
- If we have a contradiction example, we have yc =1 (we must have a contradiction span) – although we don’t know if there is a neutral span or not.
- If we have a neutral example, we have yn =1 (we must have a neutral span). We also can’t have a contradiction span, so yc=0
- Otherwise, for entailment examples, we can’t have either a neutral or a contradiction span, so both yc=0 and yn=0.
You might wonder where we get all these rules from. Can we just make them up like this? We argue that these rules follow from the inherent nature of NLI, and they just work.
The training process in the paper is a little bit more complicated than what I’ve described above, because we include an additional instance-level loss. We include this extra loss because it makes a small improvement in performance, but if you understand everything above, you understand the most important parts of the system.
The last thing to mention is that this method is model agnostic, and that you can apply this method to a range of baseline models.
The diagram below summarises how the full training process works in the paper (in this case, using a BERT model to encode the premise and each span):
Performance and limitations
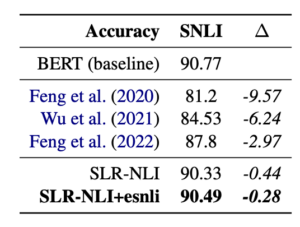
I’ve talked about the “explainability superpowers” that atomic inference methods can offer, and at this point you probably agree that it’s good to have an interpretable model. But what’s the trade-off with performance? What is the cost to get these atomic inference guarantees about model faithfulness? It turns out, there is only a small loss in performance with our system, with our method almost matching the baseline model. In contrast, other interpretable methods for SNLI show considerably worse performance.
The table below shows the performance of our method (SLR-NLI), compared to the BERT baseline, and other interpretable methods for SNLI. The results show that additional span-level supervision using the e-SNLI rationales [11] also improves performance.
At this point, we have an interpretable model, with strong faithfulness guarantees, with performance almost in-line with the baseline. Taking a step back, this seems like quite a big achievement, showing that inherently interpretable models can perform competitively compared to black-box models.
What’s the catch? There must be a catch, right? In this case, the catch is the dataset. Our atomic inference method works great for simple NLI datasets such as SNLI. But after testing our span-based method on ANLI (the focus of our 2024 paper), the results are no longer so impressive!
Atomic Inference methods for ANLI
ANLI (Adversarial NLI) is created with a human in-the-loop method where humans create challenging hypotheses that fool existing fine-tuned models. As ANLI premises are also multiple sentences, a span-level decomposition is no longer feasible (there would be too many spans), and our method of considering consecutive spans would also not work. So we need to find another way to define our atoms.
We experiment with a sentence-segmentation of the premise, which performs OK. But we find even better performance when we use an LLM to generate a list of facts to itemise all of the information contained within the premise.
You might notice that we’re now talking about decomposing an NLI premise into atoms, rather than the NLI hypothesis. Therefore, all of those training and evaluation rules we had before are no longer going to work. Is it even possible to construct such a set of training and evaluation rules that would allow us to use the same model architecture which proved so successful in our previous work? It turns out there is, and they’re summarised below (the figure is contained in our EMNLP 2024 paper Appendix if you’re interested).
I love how all these different rules just follow from the inherent nature of NLI, it just seems so elegant.
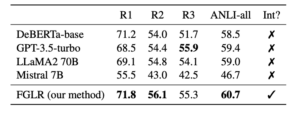
Our 2024 paper talks in more detail about how we create comprehensive fact-lists (one of the main challenges we faced). The paper then compares our method to a range of baselines (both atomic inference baselines, and uninterpretable black-box models). Surprisingly, when we implemented our interpretable fact-based method with a DeBERTa-base model, performance actually improved! Our interpretable model also outperformed some LLMs with over 100 times the number of parameters (see our results table below).
This is further evidence that, given the right choice of atoms and training framework, atomic inference models can perform competitively.
More detail about our EMNLP 2024 paper results
Now for some more detail on the results from our EMNLP 2024 paper. If you’re not interested in this level of detail, you may want to skip to the next section!
The training method we described earlier was introduced to overcome the issue where we don’t have atom-level labels during training. This was essential when dealing with text spans as atoms, when a model couldn’t be expected to make sensible predictions for text spans unless it was specifically fine-tuned to do this. This is not necessarily the case when we have facts (or sentences) as our atoms, where models trained on full premise and hypothesis NLI pairs may still be able to make accurate fact or sentence-level predictions. To test this, we train a standard ANLI model on the full premise and hypothesis pairs, and use this model to make the atom-level predictions, rather than training a model using the max supervision method we described earlier.
We find that using a standard ANLI-trained model performs worse than our training method for either sentence atoms or LLM-generated fact atoms. For sentence-atoms, our training method leads to an 1.9% accuracy improvement on ANLI. However, when we consider generated facts as atoms, the improvement from our training method is even larger (at 3.3%). This suggests that the generated facts are further from the training distribution than the sentences.
We also perform ablation experiments to understand to what extent the improvements from our method are a result of either: 1) Our training method, 2) The strategies we implement to make our fact lists more comprehensive (including an additional fact conditioned on the hypothesis). We find that both components are important.
The table below shows the performance of:
- Using the standard ANLI-trained model to make the fact-level predictions
(ablation number #1 below) - Using the standard ANLI-trained model to make a the fact-level predictions, but with the inclusion of the hypothesis-conditioned facts to make the fact lists more comprehensive
(ablation #2 below) - Using our training method (with the max supervision), but without making the facts lists more comprehensive with the hypothesis-conditioned facts
(ablation #3 below)
Interestingly, we found that if we don’t use our training method, and instead use a model trained on the full ANLI premises and hypotheses, then using sentence atoms performs better than using fact atoms. However, if we do use our training method (with the max. supervision), and we also make the fact-lists comprehensive, then using facts as atoms gives the best results!
What’s missing from our existing work, and some thoughts for future research
Atomic inference sets a high bar for interpretability. We have to break down instances into atoms, make independent predictions for each atom, these predictions must be hard predictions, and these atom-level predictions must be aggregated in an interpretable and deterministic way. Yet with the right choice of atoms, performance can still be just as good as a baseline model!
But there remains lots of work to do. First of all, I keep talking about NLI. How could this approach apply to a very different task? Perhaps for example, for the task of VQA – could you use patches as your choice of atoms? Or is there another, better choice of atom?
We also assume that either the NLI hypothesis or premise are decomposed into atoms, but what happens if we need to decompose both of these? And perhaps more importantly, are there better methods for reasoning across multiple atoms which would maintain the interpretability guarantees from atomic inference.
And finally, there is the question of model robustness. In our 2024 paper we show that existing atomic inference methods often decrease out-of-distribution performance. Is there a way to address this weakness, so we can have both interpretable and robust models that perform as well as their black-box model counterparts?
We believe this area of research is a work in progress, but atomic inference methods can be a practical and highly effective way of creating interpretable neural networks where we know exactly why the models make each prediction.
Other papers that have inspired us along the way
It would be impossible to mention all the papers that have influenced us (so I’m sorry if your paper isn’t mentioned below), but here are a select few papers that are worth reading if you enjoyed this work:
Papers that could be described as being atomic inference methods:
- Stretching Sentence-pair NLI Models to Reason over Long Documents and Clusters [6]: Decomposes a premise into sentences, with an NLI model used to predict whether hypothesis atoms are supported by a given premise statement. The ‘hard aggregation’ variant could be considered as atomic inference.
- Zero-Shot Fact Verification via Natural Logic and Large Language Models [9]: The cool thing about this paper is that the hard predictions for each atom are natural logical operators, which are then aggregated together into either ‘supports’, ‘refutes’ or ‘neither’ labels. This is an exciting idea that the atom-level label space can be different from the overall task labels.
Other relevant papers that we also particularly like:
- WiCE: Real-World Entailment for Claims in Wikipedia [7]: This work also considers an atomic fact-level decomposition, considering a mean score used to inform instance-level predictions.
- SUMMAC: Re-Visiting NLI-based Models for Inconsistency Detection in Summarization [8]: Involves decomposing a document and summary into sentences, with an NLI model providing a score for how well supported each summary sentence is. This work predates our EMNLP 2022 paper!
- PROPSEGMENT: A Large-Scale Corpus for Proposition-Level Segmentation and Entailment Recognition [3]: This paper considers a new type of atom, considering ‘propositions’ instead of sentences or facts. I love the idea about this kind of atom, and it opens the door to other ideas for how we can create atoms.
If you’re aware of other relevant papers that we haven’t cited in either our 2022 or 2024 EMNLP papers, I would love to hear from you!
Thanks for reading, and please do get in touch if you’d like to discuss any of this further. I’ll be presenting this work as a poster at EMNLP 2024 in Miami (Thursday 14th, 10:30-12:00). You can also reach me on j.stacey20@imperial.ac.uk. Thanks also to Pasquale Minervini, Haim Dubossarsky, Oana-Maria Camburu and Marek Rei for being fantastic collaborators for this work.
References:
- Joe Stacey, Pasquale Minervini, Haim Dubossarsky and Marek Rei. 2022. Logical Reasoning with Span-Level Predictions for Interpretable and Robust NLI Models. In EMNLP.
- Joe Stacey, Pasquale Minervini, Haim Dubossarsky, Oana-Maria Camburu and Marek Rei. 2024. Atomic Inference for NLI with Generated Facts as Atoms. In EMNLP.
- Sihao Chen, Senaka Buthpitiya, Alex Fabrikant, Dan Roth and Tal Schuster. 2023. PROPSEGMENT: A Large-Scale Corpus for Proposition-Level Segmentation and Entailment Recognition. In ACL Findings.
- Zijun Wu, Zi Xuan Zhang, Atharva Naik, Zhijian Mei, Mauajama Firdaus and Lili Mou. 2023. Weakly Supervised Explainable Phrasal Reasoning with Neural Fuzzy Logic. In ICLR.
- Yufei Feng, Xiaoyu Yang, Xiaodan Zhu and Michael Greenspan. 2022. Neuro-symbolic Natural Logic with Introspective Revision for Natural Language Inference. In TACL.
- Tal Schuster, Sihao Chen, Senaka Buthpitiya, Alex Fabrikant and Donald Metzler. 2022. Stretching Sentence-pair NLI Models to Reason over Long Documents and Clusters. In EMNLP Findings.
- Ryo Kamoi, Tanya Goyal, Juan Diego Rodriguez and Greg Durrett. 2023. WiCE: Real-World Entailment for Claims in Wikipedia. In EMNLP.
- Philippe Laban, Tobias Schnabel, Paul N. Bennett, Marti A. Hearst. 2022. SummaC: Re-Visiting NLI-based Models for Inconsistency Detection in Summarization. In TACL.
- Marek Strong, Rami Aly and Andreas Vlachos. 2024. Zero-Shot Fact Verification via Natural Logic and Large Language Models. In EMNLP.
- Nitay Calderon and Roi Reichart. 2024. On Behalf of the Stakeholders: Trends in NLP Model Interpretability in the Era of LLMs.
- Oana-Maria Camburu, Tim Rocktäschel, Thomas Lukasiewicz and Phil Blunsom. 2018. e-SNLI: Natural Language Inference with Natural Language Explanations. In NeurIPS